
Spēlēt Futoshiki Puzzles Online
Turpmākajā apmācībā, pamata un uzlabotas metodes, lai atrisinātu Futoshiki mīklas tiek iesniegti soli pa solim, ar pievienotajiem ilustrācijām, lai parādītu gadījuma metodes par konkrētiem valdes konfigurācijas.
Sākumpunkts risinājuma sasniegšanai ir pašas spēles definīcija: Futoshiki pieprasa lietotājam noskaidrot dēli, kurā katrs cipars parādās vienreiz katrā rindā un kolonnā, ievērojot dēļu nevienlīdzību. Izmantojot šo kritēriju, virzību uz risinājumu var panākt, soli pa solim pabeidzot tukšus dēļu laukumus ar konkrētiem cipariem, jo tie ir vienīgais veids, kā ievērot dēļu ierobežojumus.
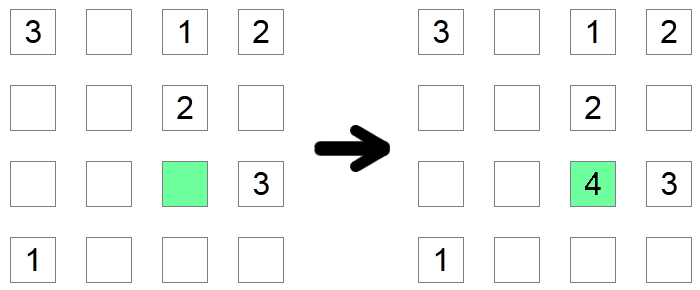
Ja kvadrātu kolonnā un rindā jau ir visi iespējamie cipari, izņemot vienu, tad šajā laukumā jābūt trūkstošajam ciparam. Iepriekš minētajā piemērā zaļajam laukumam jābūt 4, jo tam nebūtu pieļaujama nekāda cita vērtība, jo pārējie iespējamie cipari jau ir atrodami tā rindā vai kolonnā.
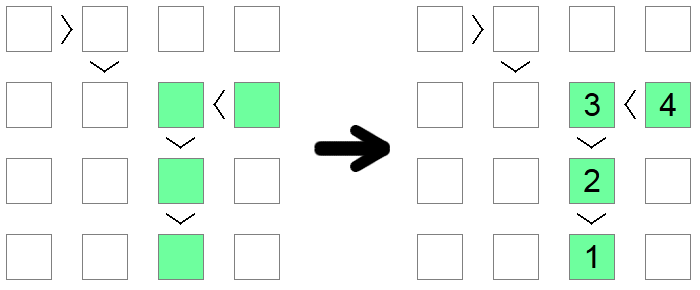
Ja pamanāt nevienādību ķēdi, vai tas ir vai nu < (visi augošā secībā) vai > (visi dilstošā secībā), kas ir vienāds ar izmēru dēļiem, tad šai ķēdei jābūt secībai no 1 līdz kuģa garumam. Ķēdes garums garantē, ka šī secība ir vienīgais iespējamais risinājums, kas atbilst nevienlīdzības ķēdes uzliktajam monotonam nosacījumam.
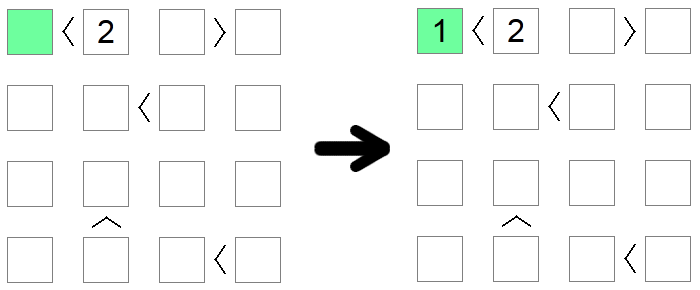
Kvadrātiem, kas ir mazāki par 2, jābūt netieši vērtībai 1, jo tā ir vienīgā pieļaujamā vērtība uz kuģa, kas atbilst šim nosacījumam. Tāpat kvadrātiem, kas ir lielāki par kuģa izmēru mīnus 1, jābūt vienādiem ar kuģa izmēru. Iepriekš minētajā piemērā vienīgā iespējamā zaļā kvadrāta vērtība (mazāk par 2) ir 1.
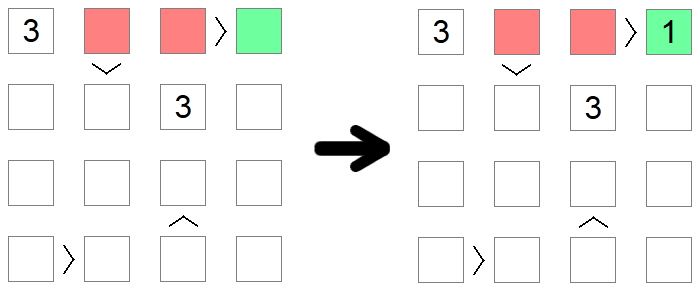
Kvadrāti, kas ir lielāki par citiem laukumiem, nevar būt 1, zemākā pieļaujamā vērtība uz kuģa, jo nav mazāka vērtība par 1. Tāpat kvadrāti, kas ir zemāki par citiem laukumiem, nevar saturēt maksimāli pieļaujamo vērtību, jo nebūtu nekā lielāka, ko aizpildīt nevienlīdzības otrā pusē. Iepriekš minētajā piemērā sarkanajos laukumos nevar aizpildīt 1, jo tie visi ir lielāki par citiem dēļu laukumiem, līdz ar to vienīgais iespējamais izvietojums 1 pirmajā dēļa rindā ir zaļais kvadrāts.
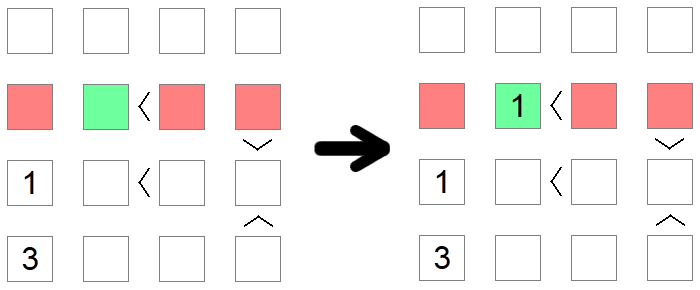
Dažreiz, lai izdarītu secinājumu, jāizmanto vairāki noteikumi. Tas ir gadījums iepriekš minētajā piemērā, kur mēs cenšamies ievietot vērtību 1 otrajā kuģa rindā. Pirmais sarkanais kvadrāts tiek likvidēts kolonnas izslēgšanas dēļ (mums jau ir 1 šajā kolonnā), bet otrais un trešais sarkanie kvadrāti tiek novērsti, jo minimālo vērtību izslēgšana, jo šīm vietām ir lielākas par nevienādībām, kas saistītas ar tām. Tāpēc zaļais kvadrāts joprojām ir vienīgā iespējamā vieta 1 ievietošanai šajā rindā.
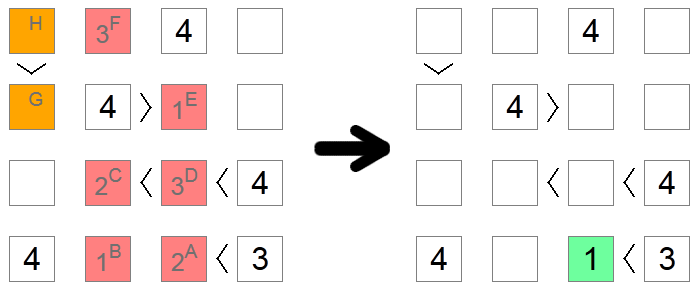
Dažreiz, it īpaši sarežģītos dēļos, nav citu veidu, kā noskaidrot pareizo ciparu kvadrātā, izņemot niršanu katras iespējas sekās, līdz tiek sasniegta pretruna. Iepriekš minētajā piemērā visi sarkanie un oranži kvadrāti sākotnēji ir tukši. Mēs vēlamies noskaidrot, vai kvadrāts A satur 1 vai 2. Mēs pieņemam, ka tajā ir 2, un mēs pārbaudām, vai mēs sasniedzam pretrunu, pamatojoties uz šo pieņēmumu.
Ja kvadrāts A ir 2, tad kvadrāts B būtu 1 (vienīgā atlikusī vērtība apakšējā rindā). Kvadrāts C var būt 1 vai 2, jo tam ir nevienādību ķēde, kas prasa, lai būtu pieejami 2 lielāki skaitļi, bet tagad tas nevar būt 1 sakarā ar laukuma B kolonnas izslēgšanu, tāpēc kvadrāts C ir a 2, bet kvadrāts D ir 3 (vienīgā vērtība starp 2 un 4). Kolonnu izslēgšanas dēļ kvadrāts E ir 1 un kvadrāts F ir 3.
Tagad, ja mēs skatāmies uz apelsīnu kvadrātu, mēs pamanām pretrunu: ja kvadrāts G būtu 2, kvadrātveida H būtu vai nu 3 vai 4, kas nav atļauti rindas izslēgšanas dēļ. Ja kvadrāts G būtu 3, kvadrātveida H būtu jābūt 4, kas nav atļauta tā paša iemesla dēļ. Tā kā mums vairs nav atlikušās vērtības kvadrātveida G, tas nozīmē, ka mēs sasniedzām strupceļu, un mūsu sākotnējais pieņēmums bija nepareizs: 2 nav derīgs solis uz kvadrātveida A, lai mēs varētu iet uz priekšu un ievietot tajā 1, vienīgo iespējamo vērtību.
Mēs esam parādījuši iepriekš, kā veiksmīgi atrisināt Futoshiki mīklu, aptverot virkni paņēmienu, kas var palīdzēt jums secināt nākamo soli pat sarežģītās situācijās. Otra galvenā sastāvdaļa, lai kļūtu lietpratējs un ātri atrisināt Futoshiki mīklas ir pieredze: jo vairāk jūs praktizēt, jo labāk un ātrāk jūs kļūsiet.
Ja jūs par izaicinājumu, jūs varat spēlēt tieši tagad izlases Futoshiki puzzle, noklikšķinot uz pogas zemāk. Veiksmi!
© 2026 - Visas tiesības aizsargātas - Par - Privātuma Politika - DE | EN | ES | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR